Sejarah Segitiga Pascal

Sejarah Segitiga Pascal

Gambaran awal tentang sebuah segi tiga pekali binomial muncul pada abad ke-10 dengan ulasan dalam Chandas Shastra, sebuah buku India purba dalam prosodi bahasa Sanskrit yang ditulis oleh Pingala antara abad ke-5–ke-2 SM. Karya Pingala pula hanya muncul tentang pecahan, yang diulas oleh Halayudha, sekitar 975, menggunakan segi tiga itu untuk menjelaskan rujukan kabur pada Meru-prastaara, “Tangga Gunung Meru”. Ia juga disedari bahawa pepenjuru pada jumlah segi tiga itu wujud pada nombor Fibonacci. ahli matematik India Bhattotpala (kk

RUMUS-RUMUS BANGUN RUANG

Rumus-rumus Bangun Ruang

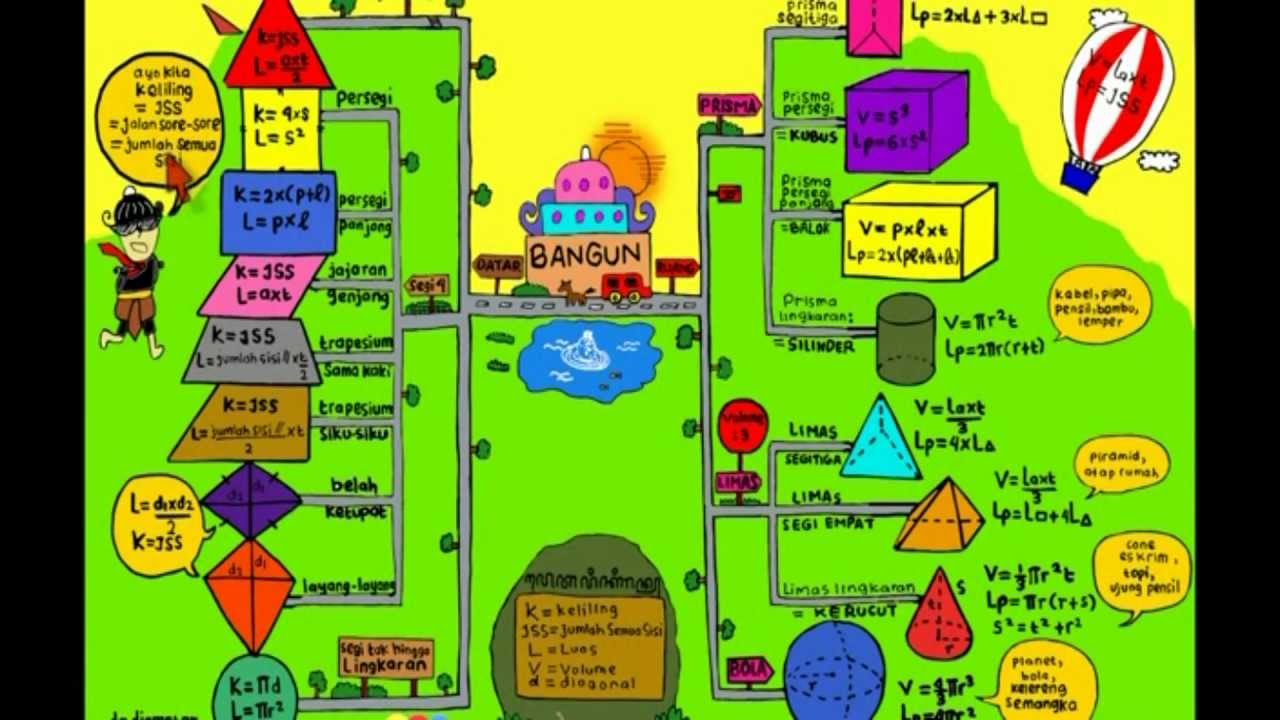ilmu matematika tidak pernah lepas dari rumus-rumus matematika mengenai bangun ruang seperti kubus, balok, kerucut, tabung, limas, dan bola. Artikel kali ini akan saya tuliskan tentang rumus bangun ruang yang ada di dalam pelajaran matematika seperti rumus kubus, rumus tabung, rumus limas, rumus kerucut,  untuk mengetahui / mempelajari / mengingat kembali luas dan volume masing-masing bangun ruang.

Bangun ruang berbeda dengan bangun datar didalam menentukan rumusnya , yaitu tergantung dari bentuk bangun masing-masing. Secara umum bentuk dari bangun ruang seperti kubus dkk adalah 3 dimensi yang mempunyai isi atau volume berbeda dengan bangun datar yang hanya 2 dimensi.

1. RUMUS BANGUN RUANG KUBUS

Kubus terdapat 6 (enam) buah sisi yang berbentuk persegi dengan luas yang sama besar diantara sisinya.
Terdapat 12 (dua belas) rusuk dengan panjang rusuk yang sama panjang.
Semua sudut bernilai 90 derajat ataupun siku-siku.


Rumus:

Luas salah satu sisi = rusuk x rusuk
Luas Permukaan Kubus = 6 x rusuk x rusuk
Keliling Kubus = 12 x rusuk
Volume Kubus = rusuk x rusuk x rusuk ( rusuk 3 )

2. RUMUS BANGUN RUANG BALOK

Rumus:

Luas Permukaan Balok = 2 x {(pxl) + (pxt) + (lxt)}
Diagonal Ruang = Akar dari (p kuadrat + l kuadrat + t kuadrat)
Keliling Balok = 4 x (p + l + t)
Volume Balok = p x l x t (sama dengan kubus, tapi semua rusuk kubus sama panjang).

3. RUMUS BANGUN RUANG BOLA 

Rumus:

Luas Bola = 4 x π x jari-jari x jari-jari, atau
                    4 x π x r2
Volume Bola = 4/3 x π x jari-jari x jari-jari x jari-jari
π  = 3,14 atau 22/7

4. RUMUS BANGUN RUANG TABUNG/SILINDER 

Rumus:


Volume = luas alas x tinggi, atau
                luas lingkaran x t
Luas = luas alas + luas tutup + luas selimut, atau
            ( 2 x π x r x r) + π x d x t)

5. RUMUS BANGUN RUANG KERUCUT 

Rumus:


Volume = 1/3 x π x r x r x t
Luas = luas alas + luas selimut

6. RUMUS BANGUN RUANG LIMAS

Rumus:

Volume = 1/3 luas alas tinggi sisi
Luas = luas alas + jumlah luas sisi tegak

Matriks

Matriks

Matriks dan Operasi-Operasinya.

Definisi : 

Matriks adalah susunan segi empat siku-siku dari bilangan yang dibatasi dengan tanda kurung. Suatu matriks tersusun atas baris dan kolom, jika matrriks tersusun atas m baris dan n kolom maka dikatakan matriks tersebut berukuran ( berordo) m x n. Penulisan matriks biasanya menggunakan huruf besar A,B,C dan seterusnya, sedangkan penulisan matriks beserta ukurannya ( matriks dengan m baris dan n kolom) adalah 

Penemu matematika

Penemu Matematika dan Awal Perkembangan Matematika di Dunia

Penemu matematika untuk pertama kalinya belum bisa dipastikan sampai saat ini. Namun untuk pertama kalinya matematikawan pertama yang merumuskan teorema atau proposisi adalah Thales (624-550 SM). Merujuk pada pemastian atas penemu matematika yang sebenarnya, sehingga terjadi beberapa pangkajian atas sejarah dari terbentuknya matematika. Cabang pengkajian yang dikenal sebagai sejarah matematika adalah penyelidikan terhadap asal mula penemuan di dalam matematika dan sedikit perluasannya, penyelidikan terhadap metode dan notasi matematika pada masa silam.

Sebelum zaman modern dan penyebaran ilmu pengetahuan ke seluruh

teori belajar

Teori- teori belajar matematika pada pembelajarannya Matematika di SD

     Teori- teori belajar matematika pada pembelajarannya Matematika di SD A. Hakikat Pembelajaran Matematika Pembelajaran matematika di SD merupakan salah satu kajian yang selalu menarik untuk di kemukakan karena adanya perbedaan karakteristik khususnya antara hakikat anak dan hakikat matematika. Anak usia SD sedang mengalami perkembangan pada tingkat berpikirnya. Ini karena tahap berpikir mereka masih belum formal. Pelajaran matematika bagi siswa SD berguna untuk kepentingan hidup pada lingkungannya , mengembangkan pola pikirnya, dan untuk mempelajari ilmu – ilmu yang kemudian. Dan pada hakikatnya pembelajaran matematika adalah proses yang sengaja dirancang dengan tujuan untukmenciptakan suasana lingkunganyang memungkinkan seseorang(sipelajar) melaksanakan kegiatanbelajar matematika.Pembelajaran matematika harusmemberikan peluang kepada siswa untuk berusaha dan mencari pengalaman tentang matematika. 

Rumus Kubus dan Balok

1. RUMUS BANGUN RUANG KUBUS

Kubus terdapat 6 (enam) buah sisi yang berbentuk persegi dengan luas yang sama besar diantara sisinya.
Terdapat 12 (dua belas) rusuk dengan panjang rusuk yang sama panjang.
Semua sudut bernilai 90 derajat ataupun siku-siku. baca juga klik disini